Fluxonium erasure qubit (to appear on arxiv soon)
Why erasure qubit: At the same total error rate, erasure errors that are mostly heralded (of known location) are easier to correct, and gives rise to higher threshold and larger logical error suppression exponent. While erasure qubits have been demonstrated on natural atoms or composite superconducting qubits, it will be cool if erasure qubit can be implemented on single-mode superconducting qubits.
We demonstrate that a single fluxonium artificial atom can be used as an erasure qubit, along with proposals for physical gates
IMSI quantum hardware workshop poster 2024
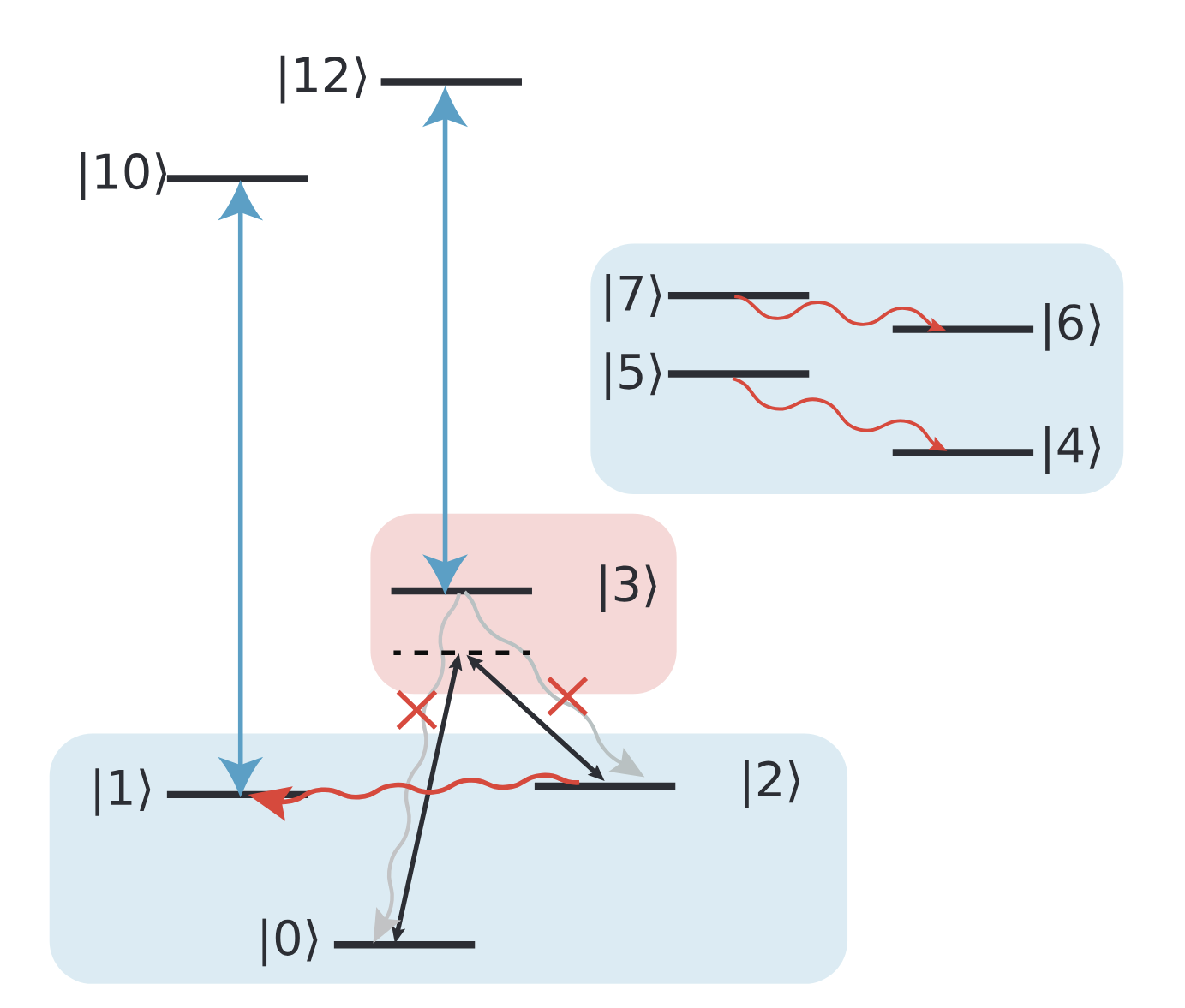
Fluxonium has a more complex potential and selection rules than transmon. We utilize the selection rule in integer fluxonium to enhance the computational subspace coherence time and do trade-off with leakage process.
a) Two-outcome leakage detection measurement via tunable resonator
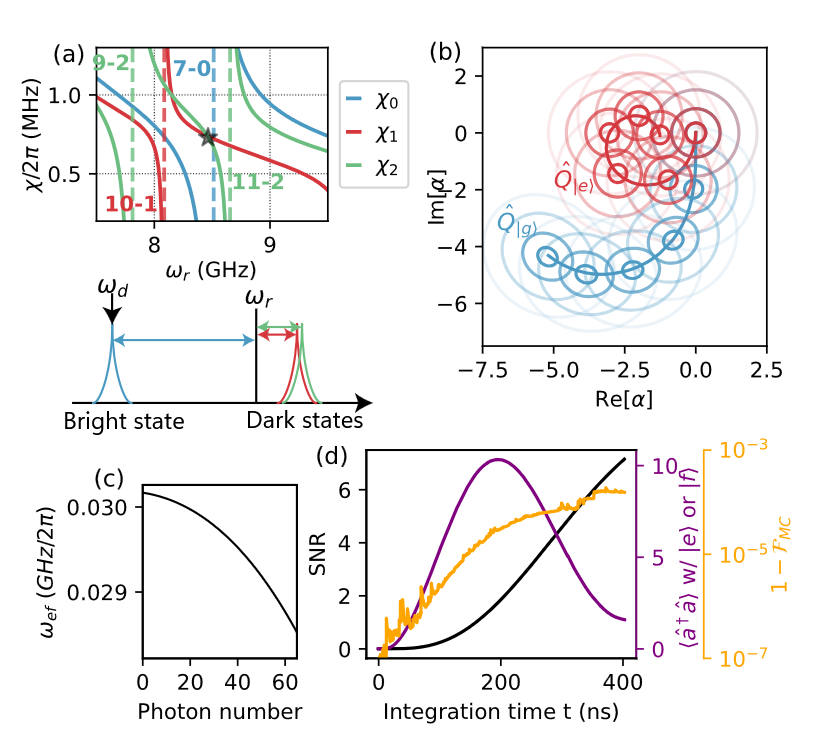
Dispersive readout can be used to detect leakage without harming qubit coherence in fluxonium. See analytical and numerical analysis on dephasing in the coming paper.
b) Two-outcome leakage detection measurement via transmon
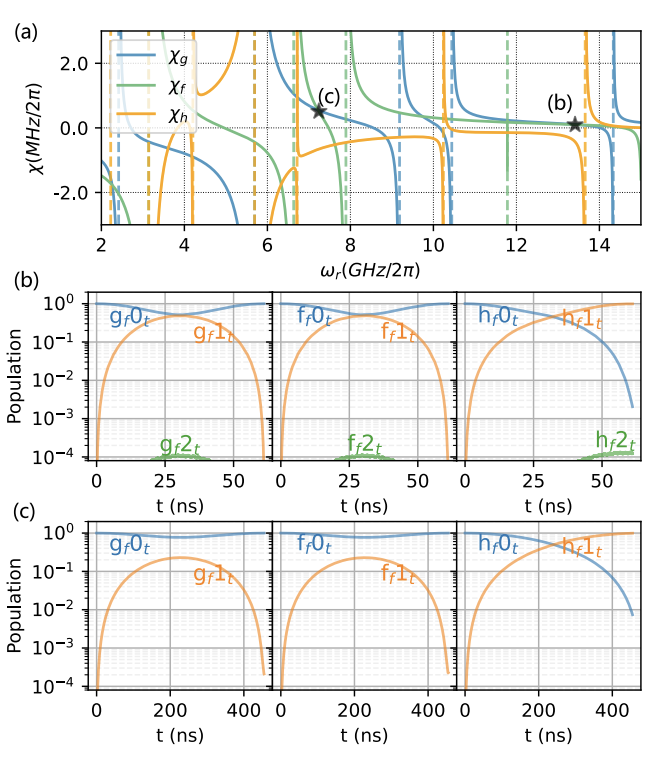
By adjusting non-linear resonator frequency and drive amplitude, we get another "degree of freedom" in the control compared to resonator based readout, making leakage detection less demanding on parameter selection.
c) “Erasure-bias” preserving gates
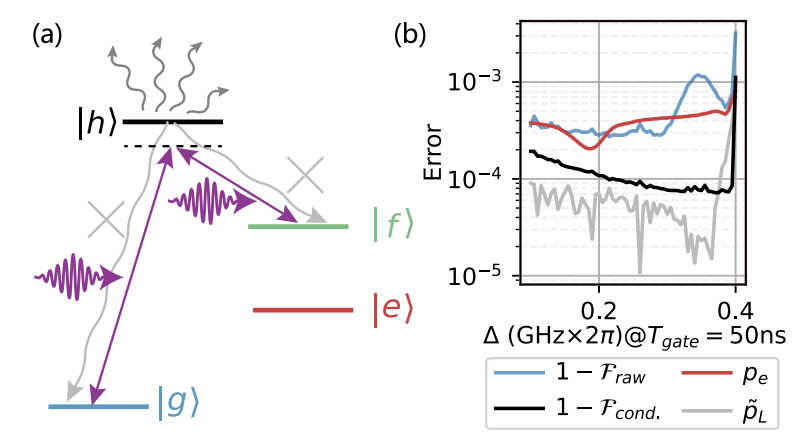
Coherence time estimation shows that g-f Integer Fluxonium Qubit (g-f IFQ) is an erasure-dominant qubit with super-long computational subspace coherence time, this feature needs to be preserve in gate operations. We show that by using large enough detuning, intermediate state decay is minimized, and additional leakage can be converted to erasure by the aforementioned leakage detection measurement via transmon. This established g-f IFQ as an erasure qubit.